网络与流 – 潘登同学的图论笔记
- 网络与流
假设 G = ( V , E ) G=(V,E) G=(V,E)是一个连通无重边且不包含自环的有向图,如果G中
(1)只有一个入度为0的顶点,记之作为s,称为源
(2)只有一个出度为0的顶点,记之作为t,称为汇
(3)每条有向边 e = ( u , v ) e=(u,v) e=(u,v)都存在一个非负权值 C u v C_{uv} Cuv,称作边的容量
则称G是一个网络或流网络,也记作 G = ( V , E , s , t , C ) G=(V,E,s,t,C) G=(V,E,s,t,C)
注:(问题转化)
①若存在重边,对重边求和作为一条边总容量
②自环的存在与否不影响问题的分析
③在实际应用中,还要考虑中转站的容量上限
④如果有多个源或者汇,那么新增两个顶点,S,T作为 源的源 和 汇的汇 ,并且将足够大的容量 C 0 C_0 C0赋予这些新加的有向边(指的是S到多个源s的边,T到多个汇t的边)
- 前驱、后继
假设顶点 v ∈ V v∈V v∈V,定义v的前驱为 p r e d ( v ) = { u ∣ ( u , v ) ∈ E } pred(v) = \{u|(u,v)∈E\} pred(v)={u∣(u,v)∈E}
定义v的后继为 s e c c ( v ) = { u ∣ ( u , v ) ∈ E } secc(v)=\{u|(u,v)∈E\} secc(v)={u∣(u,v)∈E}
- 流(流量)
若实值函数 f : E → R f: E→\mathcal{R} f:E→R满足
(1)容量限制:对所有 e = ( u , v ) ∈ E e=(u,v)∈E e=(u,v)∈E,有 f u v = f ( e ) ≤ C u v f_{uv} = f(e) ≤C_{uv} fuv=f(e)≤Cuv
(2)流量守恒:对所有顶点 v ∈ V − { s , t } , ∑ ( u ∈ p r e d ( v ) ) f u v = ∑ ( u ∈ s u c c ( v ) ) f u v v∈V-\{s,t\}, ∑_{(u∈pred(v))}f_{uv} = ∑_{(u∈succ(v))}f_{uv} v∈V−{s,t},∑(u∈pred(v))fuv=∑(u∈succ(v))fuv
则称他是网络的一个容许流分布,或简称一个流, f u v f_uv fuv称作边(u,v)上的流量,若 e = ( u , v ) e=(u,v) e=(u,v)满足 f u v = C u v f_{uv} = C_{uv} fuv=Cuv,则称e为饱和边
- 流入(出)量
对所有顶点 v ∈ V − { s } v∈V-\{s\} v∈V−{s},定义 f ( ∗ , v ) = ∑ ( u ∈ p r e d ( v ) ) f u v f( * ,v) = ∑_{(u∈pred(v))}f_{uv} f(∗,v)=∑(u∈pred(v))fuv,称作顶点v的总流入量
对所有顶点 u ∈ V − { t } u∈V-\{t\} u∈V−{t},定义 f ( u , ∗ ) = ∑ ( v ∈ p r e d ( u ) ) f u v f(u ,*) = ∑_{(v∈pred(u))}f_{uv} f(u,∗)=∑(v∈pred(u))fuv,称作顶点v的总流出量
(为完整性考虑,补充定义 f ( ∗ , s ) = 0 , f ( t , ∗ ) = 0 f(* ,s)= 0, f(t,*)= 0 f(∗,s)=0,f(t,∗)=0
流量守恒表明:流在除了元和汇以外的各个顶点的总流入等于总流出量
- 最大流
设f是网络图G的一个流, f ( s , ∗ ) f(s,*) f(s,∗)称作流f的流量,即源s的总流出量,记作|f|。若G的任意一个流f’都满足 ∣ f ∣ ≥ ∣ f ’ ∣ |f|≥|f’| ∣f∣≥∣f’∣,则称f是G的一个最大流
S-T割(非常重要)
在网络 G = ( V , E , s , t , c ) G = (V,E,s,t,c) G=(V,E,s,t,c)中,任何一个满足 s ∈ S , t ∈ T = V − S s∈S,t∈T = V-S s∈S,t∈T=V−S的顶点V的划分(S,T)称作一个S-T割,简称割
一个S-T割的容量定义为 ∑ ( u ∈ S , v ∈ T , u v ∈ E ) C u v ∑_{(u∈S,v∈T,uv∈E)}C_{uv} ∑(u∈S,v∈T,uv∈E)Cuv,记作 C u v ( S , T ) C_{uv}(S,T) Cuv(S,T)
如果图G的S-T割使得任意一个G的S-T割(S’,T’)都有 C a p ( S , T ) ≤ C a p ( S ′ , T ′ ) Cap(S,T)≤Cap(S',T') Cap(S,T)≤Cap(S′,T′)则称(S,T)是图G的一个最小S-T割,简称最小割
- 符号说明
在网络 G = ( V , E , s , t , c ) G = (V,E,s,t,c) G=(V,E,s,t,c)中,假设A、B都是V的非空子集,定义 f ( A , B ) = ∑ ( u ∈ S , v ∈ T , u v ∈ E ) f u v f(A,B) = ∑_{(u∈S,v∈T,uv∈E)}f_{uv} f(A,B)=∑(u∈S,v∈T,uv∈E)fuv,即从A穿出进入B的边的总流量,定义 C ( A , B ) = ∑ ( u ∈ A , v ∈ B , u v ∈ E ) C u v C(A,B)= ∑_{(u∈A,v∈B,uv∈E)}C_{uv} C(A,B)=∑(u∈A,v∈B,uv∈E)Cuv,即从A穿出进入B的边的总容量
(定理)割流量 = 总流量
假设 G = ( V , E , s , t , c ) G =(V,E,s,t,c) G=(V,E,s,t,c)是一个网络,令f是一个流,(S,T)是一个S-T割,则
通过该割的流量 = 由源s发出的流量;即 f ( S , T ) − f ( T , S ) = ∣ f ∣ f(S,T)-f(T,S) = |f| f(S,T)−f(T,S)=∣f∣特别地,有 f ( ∗ , t ) = ∣ f ∣ f(*, t) = |f| f(∗,t)=∣f∣
证明:(对|S|进行归纳证明)
①当 S = s S={s} S=s的时候显然成立
②假设定理对于 ∣ S ∣ < k |S|<k ∣S∣<k的时候成立;
当 ∣ S ∣ = k |S| = k ∣S∣=k时, 任取 v ∈ S − { s } v∈S-\{s\} v∈S−{s},令 S ’ = S − { v } S’= S-\{v\} S’=S−{v}, T ′ = T ∪ { v } T' = T∪\{v\} T′=T∪{v}(这一步是把S中k个对象将为k-1个,然后可以用假设)
则由 ∣ S ′ ∣ = k − 1 |S'| = k-1 ∣S′∣=k−1 可知 f ( S ’ , T ′ ) − f ( T ’ , S ’ ) = ∣ f ∣ f(S’,T')-f(T’,S’)=|f| f(S’,T′)−f(T’,S’)=∣f∣
将顶点v添加到S’后,有
$$
\begin{aligned}
f(S,T)-F(S,T) &= (f(S’,T’)-f(S’,{v})+f({v},T))-(f(T’,S’)-f(T,{v})+f(S’,{v}))\
&= f(S’,T’) - f(T’,S’) + (f({v},T) + f({v},S’)- f(T,{v}) - f(T,{v}))\
&= f(S’,T’) - f(T’,S’) + f(v,)- f(,v)\
&= f(S’,T’) - f(T’,S’) = |f|\
\end{aligned}
$$
最大流的上限由最小割决定
设G是一个网络,令f是G的一个流,(S,T)是G的一个S-T割,则 ∣ f ∣ ≤ C a p ( S , T ) |f|≤Cap(S,T) ∣f∣≤Cap(S,T)
证明: 由上面的定理
∣
f
∣
=
f
(
S
,
T
)
−
f
(
T
,
S
)
≤
f
(
S
,
T
)
=
∑
(
u
∈
S
,
v
∈
T
,
u
v
∈
E
)
f
u
v
≤
∑
(
u
∈
S
,
v
∈
T
,
u
v
∈
E
)
C
u
v
=
C
a
p
(
S
,
T
)
\begin{aligned} |f| &= f(S,T) - f(T,S)≤f(S,T)\\ &= ∑_{(u∈S,v∈T,uv∈E)}f_{uv} \\ &≤ ∑_{(u∈S,v∈T,uv∈E)}C_{uv} = Cap(S,T)\\ \end{aligned}
∣f∣=f(S,T)−f(T,S)≤f(S,T)=(u∈S,v∈T,uv∈E)∑fuv≤(u∈S,v∈T,uv∈E)∑Cuv=Cap(S,T)
推论
设G是一个网络,f是一个流,(S,T)是一个S-T割,则若 ∣ f ∣ = C a p ( S , T ) |f| = Cap(S,T) ∣f∣=Cap(S,T),则f是一个最大流且(S,T)是一个最小割
证明:假设 f 1 f_1 f1是任意一个流,则由上面定理可得, ∣ f 1 ∣ ≤ ∣ f ∣ |f_1|≤|f| ∣f1∣≤∣f∣,则 f f f是一个最大流
假设 ( S 1 , T 1 ) (S_1,T_1) (S1,T1)是任意一个S-T割,则由上面定理,可得 C a p ( S , T ) = ∣ f ∣ ≤ C a p ( S 1 , T 1 ) Cap(S,T)=|f| ≤Cap(S_1,T_1) Cap(S,T)=∣f∣≤Cap(S1,T1),因此(S,T)是一个最小S-T割
(因此只要找到最小S-T割就能找到最大流)
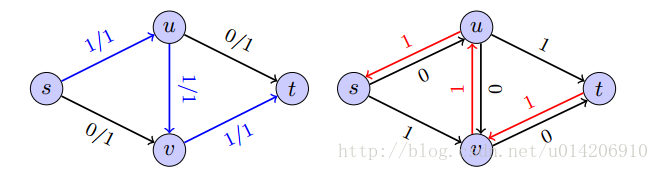
- 剩余图
假设网络 G = ( V , E , s , t , c ) G =(V,E,s,t,c) G=(V,E,s,t,c)中有流f,则可如下定义G关于f的剩余图为 G f = ( V , E , s , t , c ’ ) G_f =(V,E,s,t,c’) Gf=(V,E,s,t,c’)
(1) G f G_f Gf的顶点集与G的顶点相同
(2) G f G_f Gf的边集合 E f E_f Ef有两类: { ( u , v ) ∣ f u v < C u v } \{(u,v)|f_{uv}<C_{uv}\} {(u,v)∣fuv<Cuv},称为前向边; { ( u , v ) ∣ f v u > 0 } \{(u,v)|f_{vu}>0\} {(u,v)∣fvu>0},称为后向边;
即 E f = { ( u , v ) ∣ f u v < C u v 或 f u v > 0 } E_f = \{(u,v)|f_{uv}<C_{uv} 或 f_{uv}>0\} Ef={(u,v)∣fuv<Cuv或fuv>0}(3)容量 C u v ’ = C u v − f u v ( 当 f u v < C u v ) o r f v u ( 当 f v u > 0 ) C_{uv}’= C_{uv} - f_{uv} (当f_{uv}<C_{uv}) or f_{vu} (当f_{vu} > 0) Cuv’=Cuv−fuv(当fuv<Cuv)orfvu(当fvu>0)
(说白了就是把边反过来)
如图一个由流构造剩余图的例子:
- 可增广道路
假设网络 G = ( V , E , s , t , c ) G =(V,E,s,t,c) G=(V,E,s,t,c)中由 流 f , G 关 于 f 的 剩 余 图 流f,G关于f的剩余图 流f,G关于f的剩余图中的简单s-t道路(就是由源s到汇t的道路)P称作可增广道路,定义bottleneck(P,f)为P所经过各边的最小流量(bottleneck意思是瓶颈)
可以由增广道路P构造G的一个新流f’;
当(u,v)是P中的前向边, f u v ’ = f u v + b o t t l e n e c k ( P , f ) f_{uv}’ = f_{uv} + bottleneck(P,f) fuv’=fuv+bottleneck(P,f)
当(u,v)是P中的后向边, f u v ’ = f u v − b o t t l e n e c k ( P , f ) f_{uv}’ = f_{uv} - bottleneck(P,f) fuv’=fuv−bottleneck(P,f)
其他情况时, f u v fuv fuv
可以验证函数f’满足容量条件和守恒条件:
(1)满足容量条件。对于不在道路P上的边而言,不产生任何变化
如果(u,v)是P中的前向边, f u v ’ = f u v + b o t t l e n e c k ( P , f ) ≤ f u v + C u v ’ = f u v + C u v − f u v = C u v f_{uv}’ = f_{uv} + bottleneck(P,f)≤f_{uv} + C_{uv}’ = f_{uv} + C_{uv} - f_{uv} = C_{uv} fuv’=fuv+bottleneck(P,f)≤fuv+Cuv’=fuv+Cuv−fuv=Cuv;
如果(u,v)是P中的后向边, f u v ’ = f u v − b o t t l e n e c k ( P , f ) ≤ f u v ≤ C u v f_{uv}’ = f_{uv} - bottleneck(P,f)≤f_{uv}≤ C_{uv} fuv’=fuv−bottleneck(P,f)≤fuv≤Cuv;
(2)满足守恒条件,对于不在道路P上的顶点而言,不产生任何变化
对于在P上的顶点 v ∈ V − { s , t } v∈V-\{s,t\} v∈V−{s,t},假设在道路P上与v关联的边是(u,v)和(v,w)
①如果(u,v)和(v,w)都是P中的前向边,则
f ’ ( ∗ , v ) − f ’ ( v , ∗ ) = ( f ( ∗ , v ) + b o t t l e n e c k ( P , f ) ) − ( f ( v , ∗ ) + b o t t l e n e c k ( P , f ) ) = f ( ∗ , v ) − f ( v , ∗ ) = 0 \begin{aligned} f’(*,v) - f’(v,*) &= (f(*,v) + bottleneck(P,f)) - (f(v,*) + bottleneck(P,f))\\ &=f(*,v) - f(v,*) = 0 \end{aligned} f’(∗,v)−f’(v,∗)=(f(∗,v)+bottleneck(P,f))−(f(v,∗)+bottleneck(P,f))=f(∗,v)−f(v,∗)=0
②如果(u,v)和(v,w)都是P中的后向边,则
f
’
(
∗
,
v
)
−
f
’
(
v
,
∗
)
=
(
f
(
∗
,
v
)
−
b
o
t
t
l
e
n
e
c
k
(
P
,
f
)
)
−
(
f
(
v
,
∗
)
−
b
o
t
t
l
e
n
e
c
k
(
P
,
f
)
)
=
f
(
∗
,
v
)
−
f
(
v
,
∗
)
=
0
\begin{aligned} f’(*,v) - f’(v,*) &= (f(*,v) - bottleneck(P,f)) - (f(v,*) - bottleneck(P,f))\\ &=f(*,v) - f(v,*) = 0\\ \end{aligned}
f’(∗,v)−f’(v,∗)=(f(∗,v)−bottleneck(P,f))−(f(v,∗)−bottleneck(P,f))=f(∗,v)−f(v,∗)=0
③如果(u,v)是P中的前向边, (v,w)是P中的后向边,则
f
’
(
∗
,
v
)
−
f
’
(
v
,
∗
)
=
(
f
(
∗
,
v
)
−
b
o
t
t
l
e
n
e
c
k
(
P
,
f
)
+
b
o
t
t
l
e
n
e
c
k
(
P
,
f
)
)
−
f
(
v
,
∗
)
=
f
(
∗
,
v
)
−
f
(
v
,
∗
)
=
0
\begin{aligned} f’(*,v) - f’(v,*) &= (f(*,v) - bottleneck(P,f)+ bottleneck(P,f)) - f(v,*)\\ =f(*,v) - f(v,*) = 0\\ \end{aligned}
f’(∗,v)−f’(v,∗)=f(∗,v)−f(v,∗)=0=(f(∗,v)−bottleneck(P,f)+bottleneck(P,f))−f(v,∗)
④如果(u,v)是P中的后向边, (v,w)是P中的前向边,则
f
’
(
∗
,
v
)
−
f
’
(
v
,
∗
)
=
f
(
∗
,
v
)
−
(
f
(
v
,
∗
)
−
b
o
t
t
l
e
n
e
c
k
(
P
,
f
)
+
b
o
t
t
l
e
n
e
c
k
(
P
,
f
)
)
=
f
(
∗
,
v
)
−
f
(
v
,
∗
)
=
0
\begin{aligned} f’(*,v) - f’(v,*) &= f(*,v) - (f(v,*)- bottleneck(P,f)+ bottleneck(P,f))\\ &=f(*,v) - f(v,*) = 0\\ \end{aligned}
f’(∗,v)−f’(v,∗)=f(∗,v)−(f(v,∗)−bottleneck(P,f)+bottleneck(P,f))=f(∗,v)−f(v,∗)=0
而且 ∣ f ’ ∣ = f ’ ( s , ∗ ) = f ( s , ∗ ) + b o t t l e n e c k ( P , f ) > f ( s , ∗ ) = ∣ f ∣ |f’| = f’(s,*) = f(s,*) + bottleneck(P,f) > f(s,*) = |f| ∣f’∣=f’(s,∗)=f(s,∗)+bottleneck(P,f)>f(s,∗)=∣f∣,即流的流量得以提升
最大流,最小割定理
假设f是网络 G = ( V , E , s , t , c ) G =(V,E,s,t,c) G=(V,E,s,t,c)的一个流,则一下陈述等价
(a)f是一个最大流
(b)当且f的剩余图中不存在增广道路
©存在G的一个S-t割(S,T)使得 ∣ f ∣ = C a p ( S , T ) |f| = Cap(S,T) ∣f∣=Cap(S,T)
证明:(a)–>(b)
如果当前关于f的剩余图中存在可增广道路,则可以通过这条道路扩大流,与f是最大流矛盾
(b)–>©
假设f是不存在可增广道路的流,设S是在当前剩余图由s可达的顶点之集合,显然s∈S,且t∉S,否则存在增广道路;
令 T = V − S , 假 设 u ∈ S , v ∈ T , 若 ( u , v ) ∈ E , 则 必 有 f u v = C u v , 否 则 ( u , v ) ∈ E f T = V - S,假设u∈S,v∈T,若(u,v)∈E,则必有f_{uv} = C_{uv},否则(u,v)∈E_f T=V−S,假设u∈S,v∈T,若(u,v)∈E,则必有fuv=Cuv,否则(u,v)∈Ef,v也由s可达,与S的定义矛盾;
若 ( v , u ) ∈ E , 则 必 然 有 f v u = 0 , 否 则 ( u , v ) ∈ E f (v,u)∈E,则必然有f_{vu}=0,否则(u,v)∈E_f (v,u)∈E,则必然有fvu=0,否则(u,v)∈Ef,v也由s可达,与S的定义矛盾
©–>(a) :由上面的推论可得
(算法)Ford-Fulkerson(G) (最大流最小割算法)
输入: 网络G =(V,E,s,t,c)
输出: G的一个最大流f
①初始流量选为0流量,即对所有边 u v , f u v ← 0 uv,f_{uv}←0 uv,fuv←0
②构造G关于f的剩余图 G f G_f Gf
③若 G f G_f Gf中存在增广道路P,则按照前述方法构造由增广道路P,构造G的一个新流 f ′ f' f′, f ← f ’ f←f’ f←f’,转到②
否则输出f
(通俗来说,就是在图中随便找一条路,再把路反过来,再找一条路,再把路反过来,往复这个过程直达找不到路就是最大流了)
实现算法过程注意几点:(是我在写代码中的出来的关键)
因为f永远是正的,跟初始边的方向是同向的,所以f不需要再建一个图,直接把f并入边的属性即可cost=[f,c],所以图的数据结构要修改
增广道路的搜寻方法多种多样,可以用前面的DFS(固定起始点s,当path的最后一个元素是t时输出path即可),我这里采用BFS(广度优先搜素,详细的可以继续往后看,会说BFS)
剩余图也用同一个数据结构,但是边属性只有一个C,cost=c
接下来,还是看代码!!!冲!!!
#%%Ford-Fulkerson算法求解最大流问题
from Vertex import Vertex # 导入Vertex
from Graph import Graph # 导入之前实现的Graph
import sys
class New_Vertex(Vertex): # 某一个具体问题的数据结构需要继承原有数据结构
def __init__(self, key):
super().__init__(key)
self.color = 'white' # 新增类属性(用于记录节点是否被走过)
self.dist = sys.maxsize # 新增类属性(用于记录strat到这个顶点的距离)初始化为无穷大
self.pred = None # 顶点的前驱 BFS需要
# 新增类方法, 设置节点颜色
def setColor(self, color):
self.color = color
# 新增类方法, 查看节点颜色
def getColor(self):
return self.color
# 新增类方法, 设置节点前驱
def setPred(self, p):
self.pred = p
# 新增类方法, 查看节点前驱
def getPred(self): # 这个前驱节点主要用于追溯,是记录离起始节点最短路径上
return self.pred # 该节点的前一个节点是谁
# 新增类方法, 设置节点距离
def setDistance(self, d):
self.dist = d
# 新增类方法, 查看节点距离
def getDistance(self):
return self.dist
class New_Graph(Graph): # 继承Graph对象
def __init__(self):
super().__init__()
# 重载方法 因为原先Graph中新增节点用的是Vertex节点,但现在是用New_Vertex
def addVertex(self, key): # 增加节点
'''
input: Vertex key (str)
return: Vertex object
'''
if key in self.vertList:
return
self.numVertices = self.numVertices + 1
newVertex = New_Vertex(key) # 创建新节点
self.vertList[key] = newVertex
return newVertex
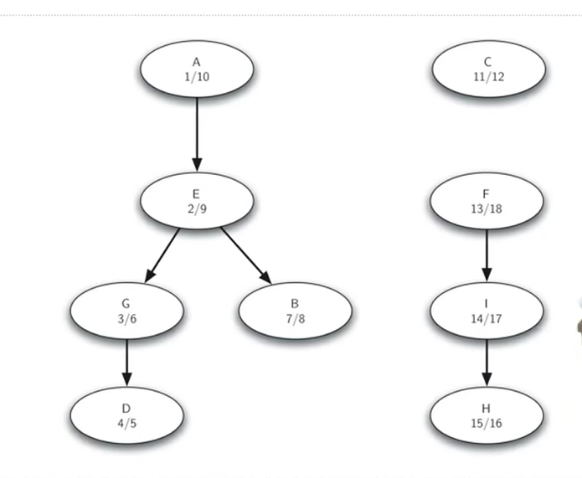
# %广度优先算法(先从距离为1开始搜索节点,搜索完所有距离为k才搜索距离为k+1)
'''
为了跟踪顶点的加入过程,并避免重复顶点,要为顶点增加三个属性
距离distance:从起始顶点到此顶点路径长度
前驱顶点predecessor:可反向追随到起点
颜色color:标识了此顶点是尚未发现(白色),已经发现(灰色),还是已经完成探索(黑色)
还需用一个队列Queue来对已发现的顶点进行排列
决定下一个要探索的顶点(队首顶点)
BFS算法过程
从起始顶点s开始,作为刚发现的顶点,标注为灰色,距离为0,前驱为None,
加入队列,接下来是个循环迭代过程:
从队首取出一个顶点作为当前顶点;遍历当前顶点的邻接顶点,如果是尚未发现的白
色顶点,则将其颜色改为灰色(已发现),距离增加1,前驱顶点为当前顶点,加入到队列中
遍历完成后,将当前顶点设置为黑色(已探索过),循环回到步骤1的队首取当前顶点
'''
# 队列 -- 也是BFS需要的
class Queue:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def enqueue(self, items): # 往队列加入数据
self.items.insert(0, items)
def dequeue(self):
return self.items.pop()
def size(self):
return len(self.items)
class max_flow_graph():
# 创建图和初始化流f
# 注意图中的cost由[flow, cost] 组成 前者表示流量 后者表示容量
# 既可以传入字典也能传入邻接矩阵
def createGraph_f(self, g_dict=None, g_matrix=None):
'''
input: g_dict(邻接表) or g_matrix(邻接矩阵)
output: directgraph(有向图)
'''
graph = New_Graph()
# f = Graph()
if g_dict:
for from_key in g_dict:
for to_key in g_dict[from_key]:
# 这里就是注意提到的f跟着c走所以原图的c是[f,c],这个很重要
graph.addEdge(from_key, to_key[0], [0, to_key[1]])
elif g_matrix:
# 先给顶点起个名字
name = [str(i) for i in range(1, len(g_matrix)+1)]
for i, from_key in enumerate(name):
for j, to_key in enumerate(name):
if g_matrix[i][j] != float('inf'):
graph.addEdge(from_key, to_key, [0,g_matrix[i][j]])
return graph
# 得到简单的s-t道路P
def BFS(self, gf, start, end): # g是图,start是起始的节点
'''
g: Gf 剩余图
start: key
end: key
return: p 以节点为元素的道路列表
'''
start.setDistance(0) # 距离
start.setPred(None) # 前驱节点
vertQueue = Queue() # 队列
vertQueue.enqueue(start) # 把起始节点加入图中
while vertQueue.size() > 0: # 当搜索完所有节点时,队列会变成空的
currentVert = vertQueue.dequeue() # 取队首作为当前顶点
for nbr in currentVert.getConnections(): # 遍历临接顶点
if (nbr.getColor() == 'white'): # 当邻接顶点是灰色的时候
nbr.setColor('gray')
nbr.setDistance(currentVert.getDistance() + 1)
nbr.setPred(currentVert)
vertQueue.enqueue(nbr)
currentVert.setColor('balck')
P = []
P.append(end)
while end.getPred():
end = end.getPred()
P.append(end)
return P[::-1]
# 由原图构造剩余图
def create_remain_graph(self, g):
'''
input: g有向图(包含flow流量和cost容量)
output: gf剩余图(就是把flow的方法反过来的一个图)
'''
# 剩余图gf的边只有一个属性就是cost
gf = New_Graph()
# 获得顶点集
verlist = g.vertList
for i in verlist:
from_key = verlist[i]
gf.addVertex(from_key.getId())
for to_key in from_key.getConnections():
gf.addVertex(to_key.getId())
f = from_key.getWeight(to_key)[0] # f表示流
c = from_key.getWeight(to_key)[1] # c表示容量
# 前向边
if f < c:
c_new = c - f
gf.addEdge(from_key.getId(), to_key.getId(), c_new)
# 后向边
if f > 0:
gf.addEdge(to_key.getId(), from_key.getId(), f)
return gf
def print_flow(self, g):
'''
input: g 带流的图
output: flow_matrix
'''
result = [[0]*len(g) for _ in range(len(g))]
for i in range(1, len(g)):
from_key = str(i)
for j in range(i+1, len(g)+1):
to_key = str(j)
from_Vertex = g.getVertex(from_key)
to_Vertex = g.getVertex(to_key)
try:
result[i-1][j-1] = from_Vertex.getWeight(to_Vertex)[0]
except:
pass
return result
def Ford_Fulkerson(self, g):
'''
算法主流程:
1.初始化流为0 (f<--0)(我把这步放到createGraph中了)
2.构造G关于f的剩余图gf
3.若gf中存在增广道路P, 则由增广道路P构造G的一个新流f’
f <-- f' 转步骤2
否则输出f
Parameters
----------
g : graph
由createGraph_f创建的图.
Returns
-------
choice matrix
流量方案的选择(每一行表示一个流出点, 每一列表示一个流入点).
'''
# 构造g关于f的剩余图Gf
gf = self.create_remain_graph(g)
# 求出Gf的增广道路
P = self.BFS(gf, gf.getVertex('1'), gf.getVertex(str(len(g))))
# 若存在增广道路 则由增广道路构造G的一个新流f
while len(P)>1:
# 计算增广路中的bottleneck
bottleneck = 1e5
for i in range(len(P)-1):
if P[i].getWeight(P[i+1]) < bottleneck:
bottleneck = P[i].getWeight(P[i+1])
# 更新f
for i in range(len(P)-1):
u_name = P[i].getId()
v_name = P[i+1].getId()
u = g.vertList[u_name]
v = g.vertList[v_name]
c = u.getWeight(v)
# 如果(u,v)是g中的正向边
if v in u.getConnections():
c[0] += bottleneck
elif u in v.getConnections():
c[0] -= bottleneck
# 流一定是正向的,只有剩余图的边有可能是反向的
g.addEdge(u_name, v_name, c)
# 更新gf
gf = self.create_remain_graph(g)
# 求出Gf的增广道路
P = self.BFS(gf, gf.getVertex('1'), gf.getVertex(str(len(g))))
return self.print_flow(g)
if __name__ == '__main__':
g_dict ={'1':[['2', 10], ['3', 10]],
'2':[['3', 2], ['4', 4], ['5', 8]],
'3':[['5', 9]],
'4':[['6', 10]],
'5':[['4', 6], ['6', 10]]}
s = max_flow_graph()
g = s.createGraph_f(g_dict)
print(s.Ford_Fulkerson(g))
(注:如果各边的容量都是整数,则每次f←f‘的更新都使得流的值至少增加1,因此算法至多再 ∑ ( v ∈ s u s s ( s ) C s v ∑_{(v∈suss(s)}C_{sv} ∑(v∈suss(s)Csv次结束,如果各边的容量是一般实数,那么该算法永远运行下去)
- 网络最大流的应用
可以将二部图的匹配问题转化为网络流图
步骤:(1)将原图所有无向边改为有向边,由X中顶点指向Y中顶点
(2)添加一个超源顶点S和一个超汇顶点T
(3)添加S到X中每个顶点的有向边,添加Y中每个顶点到T的有向边
(4)所有有向边的容量都设置为1
所得的图称作匹配网络,显然二部图中的最大匹配对应匹配网络的最大流。(看到这里是不是豁然开朗了,原来网上说的二部图的最大匹配算法的原理是这样)
我的离散数学的图论笔记就到此为止了!!,如果你也是一个证明一个证明看下来,一行代码一行代码地敲下来的话,你已经很强啦!!!