文章目录
图是什么?
图是由顶点集合及顶点间的关系组成的一种数据结构:
G = (V, E),其中V表示顶点的集合,E表示边的集合(表示顶点间的关系),这两个集合都是又穷非空的集合。
- 有向图和无向图:在有向图中,顶点对<x, y>是有序的,顶点对<x, y>称为顶点x到顶点y的一条边,<x, y>和<y, x>是两条不同的边;而在无向图中则相反,从x到y的边或者是从y到x的边,都是同一条边(没有特定方向的)。在做算法题的时候,我们在做无向图经常会在两个顶点之间连两条有向边来表示无向边。
- 完全图:在有n个顶点的无向图中,若有n * (n - 1) / 2条边,即任意两个顶点之间有且仅有一条边,则成此图为无向完全图;在n个顶点的有向边中,若有n * (n + 1)条边,即任意两个顶点之间有且仅有方向相反的边,则称此图为有向完全图。
- 邻接顶点:在无向图G中,若(u, v)是E(G)中的一条边,则称u和v互为邻接顶点,并称边(u, v)依附于顶点u和v;在有向图G中,若<u, v>是E(G)中的一条边,则称顶点u邻接到v,顶点v邻接自顶点u,并称边<u, v>与顶点u和顶点v相关联。
- 顶点的度:顶点v的度是指与它相关联的边的条数,记作deg(v)。在有向图中,顶点的度等于该顶点的入度与出度的和;但是对于无向图来说,不存在入度和出度一说,所以顶点的度就是与之连接的边数。
- 路径:在图中,若从顶点vi出发有一组边可以使其到达顶点vj,则称顶点vi到顶点vj的顶点序列为冲顶点vi到顶点vj的路径。
- 路径长度:对于不带权图,一条路径的长度就是该路径上边的数量;对于带权图,一条路径的长度就是该路径上每条边权值的总和。
- 连通图:在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的,那么就可以证明这个图就是连通图。
- 强连通图:在有向图中,若在每一对顶点vi和vj之间都存在一条从vi到vj的路径,也存在从vj到vi的路径,那么就说这个图是强连通图。
- 生成树:一个连通图的最小联通子图称作这个图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边。(具体后面会总结到)
图的存储
由于图是既有节点又有边的,所以在图存储的过程中就需要保存节点和边的关系。节点的保存与前面其他数据结构是类似的,这里就不做总结,此外,边(包含两个节点之间的关系)需要如何存储呢?下面总结会使用到的两种方式。
邻接矩阵
因为节点和节点之间的关系就是是否连通(定义成0或者1),所以这种方式存储图的话会先用一个数组(或哈希表)将顶点保存,之后使用邻接矩阵(二维数组)来表示节点和节点之间的关系。
注意:无向图的邻接矩阵是对称的,而有向图则不一定是对称的,因为入度和出度不一定是相对的。如果边是带有权值的,并且两个节点之间是连通的,那么邻接矩阵中边的关系就使用权值来进行代替,如果两个节点之间是不连通的,则将对应位置置为无穷大即可。
public class GraphByMatrix {
private Map<Character, Integer> mapV; //顶点数组
private int[][] matrix; //邻接矩阵
private boolean isDirect; //是否是有向图
/**
* @param size 代表当前定点个数
* @param isDirect 代表是否是有向图
*/
public GraphByMatrix(int size, boolean isDirect){
this.mapV = new HashMap<>();
this.matrix = new int[size][size];
for(int i = 0; i < size; i++){
Arrays.fill(matrix[i], Integer.MAX_VALUE);
}
this.isDirect = isDirect;
}
public void initArrayV(char[] array){
for(int i = 0; i < array.length; i++){
mapV.put(array[i], i);
}
}
public void addEdge(char srcV, char destV, int weight){
int srcIndex = getIndexV(srcV);
int destIndex = getIndexV(destV);
matrix[srcIndex][destIndex] = weight;
if(isDirect == false){
matrix[destIndex][srcIndex] = weight; //如果是无向图则需要进行对称
}
}
//获取定点的下标
private int getIndexV(char v){
if(mapV.containsKey(v)){
return mapV.get(v);
}
return -1;
}
//获取顶点的度
public int getDevOfV(char v){
int cnt = 0;
int srcIndex = getIndexV(v);
//出度
for(int i = 0; i < mapV.size(); i++){
if(matrix[srcIndex][i] != Integer.MAX_VALUE){
cnt++;
}
}
//有向图还需要计算入度
if(isDirect){
for(int i = 0; i < matrix.length; i++){
if(srcIndex == i) continue;
for(int j = 0; j < matrix[i].length; j++){
if(matrix[j][srcIndex] != Integer.MAX_VALUE){
cnt++;
}
}
}
}
return cnt;
}
}
邻接表
邻接表相对来说就会比较麻烦,同样使用数组(或哈希表)来表示顶点的集合,但是对边的存储使用的是链表。
无向图邻接表存储
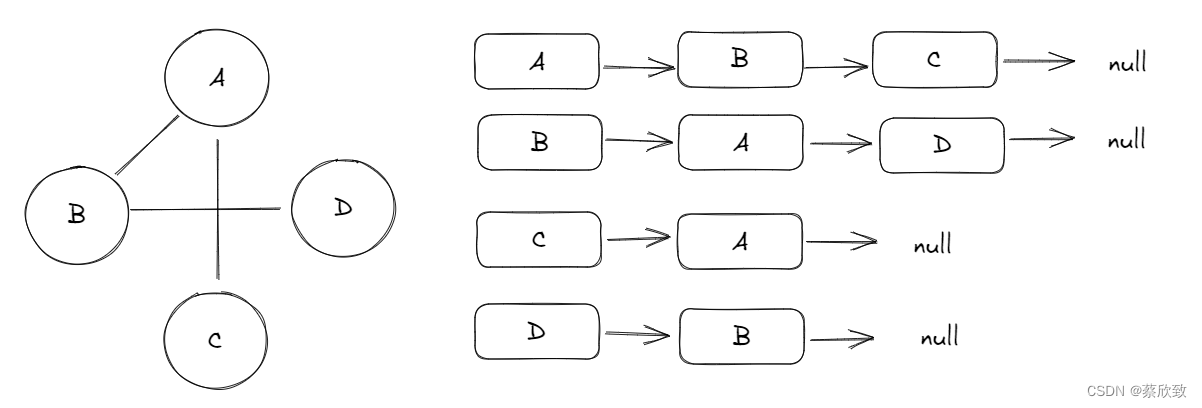
此时的图就可以使用链表的形式这样存储,这样的好处在于如果想要知道某个顶点的度,那么可以直接看它链表节点的个数即可。
有向图邻接表存储
对于有向图的话,在创建链表的时候则需要考虑方向的问题,而且在获取某个顶点的度的时候就不能再像无向图那样仅仅只是看链表节点的个数,因为有向图是有入度和出度,所以还需要在其他链表上遍历看看是否有存在词节点。
public class GraphByNode {
static class Node{
public int src; //起始位置
public int dest; //目标位置
public int weight;
public Node next;
public Node(int src, int dest, int weight){
this.src = src;
this.dest = dest;
this.weight = weight;
}
}
public Map<Character, Integer> mapV;
public List<Node> edgeList; //存储边
public boolean isDirect;
public GraphByNode(int size, boolean isDirect){
this.mapV = new HashMap<>();
this.edgeList = new ArrayList<>();
for(int i = 0; i < size; i++){
this.edgeList.add(null);
}
this.isDirect = isDirect;
}
public void initArrayV(char[] array){
for(int i = 0; i < array.length; i++){
mapV.put(array[i], i);
}
}
public void addEdge(char srcV, char destV, int weight){
int scrIndex = getIndexV(srcV);
int destIndex = getIndexV(destV);
addEdgeChild(scrIndex, destIndex, weight);
if(isDirect == false){ //无向图需要添加两条边
addEdgeChild(destIndex, scrIndex, weight);
}
}
private void addEdgeChild(int srcIndex, int destIndex, int weight){
Node cur = edgeList.get(srcIndex);
while(cur != null){
if(cur.dest == destIndex) return;
cur = cur.next;
}
Node node = new Node(srcIndex, destIndex, weight);
node.next = edgeList.get(srcIndex);
edgeList.set(srcIndex, node);
}
//获取定点的下标
private int getIndexV(char v){
if(mapV.containsKey(v)){
return mapV.get(v);
}
return -1;
}
//获取顶点的度
public int getDevOfV(char v){
int cnt = 0;
int srcIndex = getIndexV(v);
Node cur = edgeList.get(srcIndex);
while(cur != null){
cnt++;
cur = cur.next;
}
if(isDirect){
int destIndex = srcIndex;
for(int i = 0; i < mapV.size(); i++){
if(i == destIndex) continue;
Node node = edgeList.get(i);
while(node != null){
if(node.dest == destIndex){
cnt++;
}
node = node.next;
}
}
}
return cnt;
}
}
总结:在做算法题中,一般都是使用邻接表来存储的,因为实现起来会比较简单,下面是算法中实现邻接表的模板以及加边操作:
public static int[] h = new int[N]; //存储链表头结点
public static int[] e = new int[N]; //存储节点
public static int[] ne = new int[N]; //存储下一个节点
public static int idx = 0;
//加边操作(添加一条边a->b)
public static void add(int a, int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
public static void main(String[] args){
Arrays.fill(h, -1); //初始化
}
图的遍历
图的遍历有两种:广度优先遍历(BFS)和深度优先遍历(DFS)。
广度优先遍历(BFS)
图的广度优先遍历其实就类似与树中的层序遍历,以一个节点为起始点,每次往其子节点遍历,一层一层直到遍历完,对于树来说是子节点,那对于图来说其实就是要去邻接矩阵中查看,如果对应位置上(起始点对应的邻接矩阵那一行)不是无穷大(存在边)同时没有被使用过,那么就可以将其加入到队列中。
//广度优先遍历
public void bfs(char v){
boolean[] visited = new boolean[mapV.size()];
Queue<Integer> queue = new LinkedList<>();
int srcIndex = getIndexV(v);
queue.offer(srcIndex);
while(!queue.isEmpty()){
int top = queue.poll();
for(Character key : mapV.keySet()){
if(mapV.get(key) == top){
System.out.print(key + " ");
}
}
visited[top] = true;
for(int i = 0; i < matrix[0].length; i++){
if(matrix[top][i] != Integer.MAX_VALUE && visited[i] == false){
queue.offer(i);
visited[i] = true;
}
}
}
}
算法题中实现的模板:
public static void bfs(){
Queue<Integer> queue = new LinkedList<>();
st[1] = true;
queue.offer(1);
while(!queue.isEmpty()){
int t = queue.poll();
for(int i = h[t]; i != -1; i = ne[i]){
int j = e[i];
if(!st[j]){
st[j] = true;
queue.offer(j);
}
}
}
}
深度优先遍历(DFS)
图的深度优先遍历其实就类似与树中的前序遍历,不断递归查找到叶节点后回溯,直到将整棵树都遍历完。
//深度优先遍历
public void dfs(char v){
boolean[] visited = new boolean[mapV.size()];
int srcIndex = getIndexV(v);
dfsChild(srcIndex, visited);
}
private void dfsChild(int srcIndex, boolean[] visited){
for(Character key : mapV.keySet()){
if(mapV.get(key) == srcIndex){
System.out.print(key + " ");
}
}
visited[srcIndex] = true;
for(int i = 0; i < matrix[0].length; i++){
if(matrix[srcIndex][i] != Integer.MAX_VALUE && visited[i] == false){
dfsChild(i, visited);
}
}
}
算法题中实现的模板:
public static int dfs(int u){
st[u] = true;
for(int i = h[u]; i != -1; i = ne[i]){
int j = e[i];
if(!st[j]) dfs(j);
}
}
最小生成树
先简单说一下生成树的概念:在连通图中的每一颗生成树都是原图的一个极大无环子图(从其中删去任何一条边,生成树就不再连通;反之,在其中引入任意一条新的边,都会形成一条回路)。
如果连通图是由n个顶点组成的,那么它的生成树必须是含n个顶点和n-1条边,因此构成最小生成树的准则有三条:1. 只能使用图中的边来构造最小生成树;2. 只能使用恰好n-1条边来连接图中的n个顶点;3. 选用的n-1条边不能构成回路;4. 路径构成的权值是最小的。
其中,构造最小生成树的方法主要有两种:Kruskal算法和Prim算法,这两个算法都是采用了逐步求解的贪心策略。
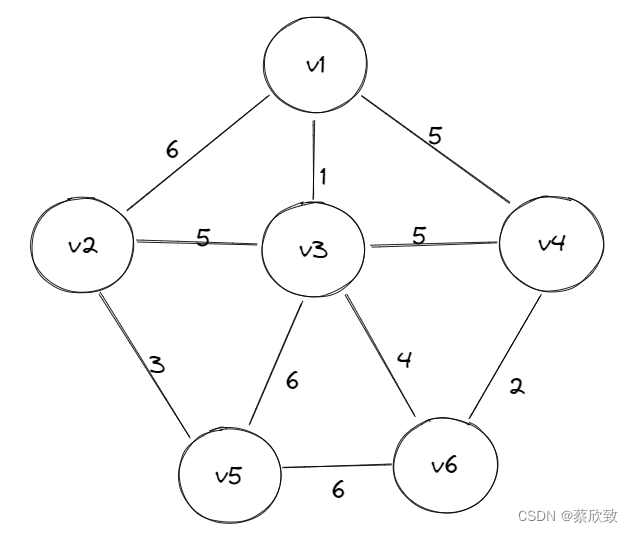
Prim算法
Prim算法是一种局部贪心的算法,每次选出一条最短路径之后,会将新增的节点加入到集合中,再在看这个集合周围连接的边选择符合准则下的一条最小边,一直贪心选边,最后就会构成最小生成树。以上面那个连通图为例,简单画一下Prim算法的执行流程:
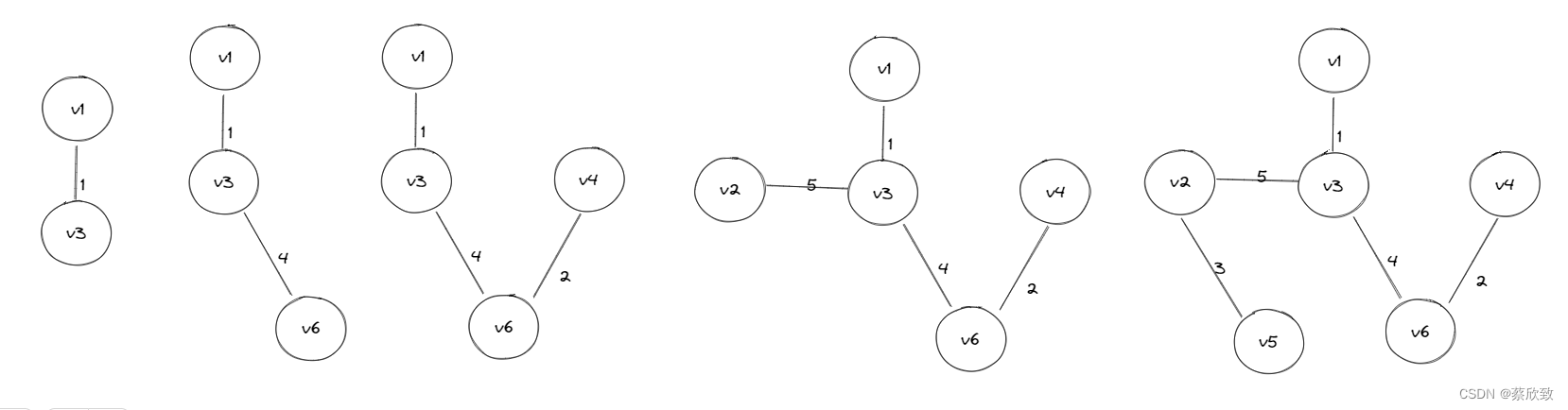
static class Edge{
public int srcIndex;
public int destIndex;
public int weight;
public Edge(int srcIndex, int destIndex, int weight){
this.srcIndex = srcIndex;
this.destIndex = destIndex;
this.weight = weight;
}
}
private void addEdgeByIndex(int srcIndex, int destIndex, int weight){
matrix[srcIndex][destIndex] = weight;
if(isDirect == false){
matrix[destIndex][srcIndex] = weight; //如果是无向图则需要进行对称
}
}
public int prim(GraphByMatrix minTree, char chV){
int srcIndex = getIndexV(chV);
Set<Integer> setX = new HashSet<>(); //存储已经确定的点
setX.add(srcIndex);
Set<Integer> setY = new HashSet<>(); //存储不确定的点
int n = matrix.length;
for(int i = 0; i < n; i++){
if(i != srcIndex) setY.add(i);
}
PriorityQueue<Edge> minQueue = new PriorityQueue<>(new Comparator<Edge>() {
@Override
public int compare(Edge o1, Edge o2) {
return o1.weight - o2.weight;
}
});
for(int i = 0; i < n; i++){
if(matrix[srcIndex][i] != Integer.MAX_VALUE){
minQueue.offer(new Edge(srcIndex, i, matrix[srcIndex][i]));
}
}
int size = 0;
int totalWeight = 0;
while(!minQueue.isEmpty()){
Edge min = minQueue.poll();
int srcI = min.srcIndex;
int destI = min.destIndex;
if(!setX.contains(destI)) {
minTree.addEdgeByIndex(srcI, destI, min.weight);
size++;
totalWeight += min.weight;
if(size == n - 1) return totalWeight;
//更新集合
setX.add(destI);
setY.remove(destI);
//将destI连接出去的所有边都放到优先级队列中
for(int i = 0; i < n; i++){
if(matrix[destI][i] != Integer.MAX_VALUE && !setX.contains(i)){
minQueue.offer(new Edge(destI, i, matrix[destI][i]));
}
}
}
}
return -1;
}
提醒:使用Prim算法比较适用于节点少的情况。
Kruskal算法
Kruskal算法是一种全局贪心的算法,使用这种算法的前提是需要先知道图中所有边的权重,之后每次在符合准则的条件下选择出最短的那条路径,直到最后就构成最小生成树。以上面那个连通图为例,简单画一下Kruskal算法的执行流程:

static class Edge{
public int srcIndex;
public int destIndex;
public int weight;
public Edge(int srcIndex, int destIndex, int weight){
this.srcIndex = srcIndex;
this.destIndex = destIndex;
this.weight = weight;
}
}
private void addEdgeByIndex(int srcIndex, int destIndex, int weight){
matrix[srcIndex][destIndex] = weight;
if(isDirect == false){
matrix[destIndex][srcIndex] = weight; //如果是无向图则需要进行对称
}
}
//最小生成树(返回权值总和)
public int kruskal(GraphByMatrix minTree){
PriorityQueue<Edge> minQueue = new PriorityQueue<>(new Comparator<Edge>() {
@Override
public int compare(Edge o1, Edge o2) {
return o1.weight - o2.weight;
}
});
//遍历邻接矩阵,将边存到优先级队列中
for(int i = 0; i < matrix.length; i++){
for(int j = 0; j < matrix[0].length; j++){
if(i < j && matrix[i][j] != Integer.MAX_VALUE){
minQueue.offer(new Edge(i, j, matrix[i][j]));
}
}
}
UnionFindSet unionFindSet = new UnionFindSet(matrix.length);
int size = 0;
int totalWeight = 0;
while(size < matrix.length && !minQueue.isEmpty()){
Edge edge = minQueue.poll();
int srcIndex = edge.srcIndex;
int destIndex = edge.destIndex;
if(!unionFindSet.isSameUnionFindSet(srcIndex, destIndex)){
minTree.addEdgeByIndex(srcIndex, destIndex, edge.weight);
size++; //记录下添加边的条数
totalWeight += edge.weight;
unionFindSet.union(srcIndex, destIndex);
}
}
if(size == matrix.length - 1){
return totalWeight;
}
return -1; //没有最小生成树
}
提醒:使用Kruskal算法比较适用于边数少的情况。
最短路径问题
最短路径问题其实就是从在带权图的某一顶点出发,找出一条通往另一个顶点的最短路径,最短也就是沿路径各边的权值总和达到最小。
Dijkstra算法(求单源最短路径)
Dijkstra算法存在的问题是不支持图中带负权的路径,如果带有负权的路径,就有可能会找不到一些路径的最短路。时间复杂度是O(n^2)。
public void dijkstra(char vSrc, int[] dest, int[] pPath){
int srcIndex = getIndexV(vSrc);
Arrays.fill(dest, Integer.MAX_VALUE);
dest[srcIndex] = 0;
Arrays.fill(pPath, -1);
pPath[srcIndex] = 0;
int n = matrix.length;
boolean[] s = new boolean[n];
for(int k = 0; k < n; k++){
int min = Integer.MAX_VALUE;
int u = srcIndex;
for(int i = 0; i < n; i++){
if(s[i] == false && dest[i] < min){
min = dest[i];
u = i;
}
}
s[u] = true;
//松弛u连接出去的所有顶点v
for(int v = 0; v < n; v++){
if(s[v] == false && matrix[u][v] != Integer.MAX_VALUE && dest[u] + matrix[u][v] < dest[v]){
dest[v] = dest[u] + matrix[u][v];
pPath[v] = u;
}
}
}
}
public static int n;
public static int[] w = new int[N];
public static int[] h = new int[N]; //存储链表头结点
public static int[] e = new int[N]; //存储节点
public static int[] ne = new int[N]; //存储下一个节点
public static int idx = 0;
public static int[] dist = new int[N]; //存储所有点到1号点的距离
public static boolean[] st = new int[N]; //存储每个点的最短距离是否已经确定
public static int dijkstra(){
Arrays.fill(dist, 0x3f3f3f3f);
dist[1] = 0;
PriorityQueue<int[]> queue = new PriorityQueue<>((o1,o2)->o1[0]-o2[0]);
queue.offer(new int[]{0, 1});
while(!queue.isEmpty()){
int[] tmp = queue.poll();
int d = tmp[0], t = tmp[1];
if(st[t]) continue;
st[t] = true;
for(int i = h[t]; i != -1; i = ne[i]){
int j = e[i];
if(dist[j] > d + w[i]){
dist[j] = d + w[i];
queue.offer(new int[]{dist[j], j});
}
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
Bellman-Ford算法(求单源最短路径)
Bellman-Ford算法解决了Dijkstra算法中存在不支持图中带负权的路径问题。但是时间复杂度是O(n^3)。
public boolean ford(char vSrc, int[] dest, int[] pPath){
int srcIndex = getIndexV(vSrc);
Arrays.fill(dest, Integer.MAX_VALUE);
dest[srcIndex] = 0;
Arrays.fill(pPath, -1);
pPath[srcIndex] = 0;
int n = matrix.length;
for(int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] != Integer.MAX_VALUE && dest[i] + matrix[i][j] < dest[j]) {
dest[j] = dest[i] + matrix[i][j];
pPath[j] = i;
}
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] != Integer.MAX_VALUE && dest[i] + matrix[i][j] < dest[j]) {
return false;
}
}
}
return true;
}
Floyd算法(求多源最短路径)
public void floyd(int[][] dest, int[][] pPath){
int n = matrix.length;
for(int i = 0; i < n; i++){
Arrays.fill(dest[i], Integer.MAX_VALUE);
Arrays.fill(pPath[i], -1);
}
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
if(matrix[i][j] != Integer.MAX_VALUE){
dest[i][j] = matrix[i][j];
pPath[i][j] = i;
}else{
pPath[i][j] = -1;
}
if(i == j){
dest[i][j] = 0;
pPath[i][j] = -1;
}
}
}
for(int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dest[i][k] != Integer.MAX_VALUE && dest[k][j] != Integer.MAX_VALUE && dest[i][k] + dest[k][j] < dest[i][j]) {
dest[i][j] = dest[i][k] + dest[k][j];
//更新父节点下标
pPath[i][j] = pPath[k][j];
}
}
}
}
}